DADA2

题目：dada2: high-resolution sample inference from illumina amplicon datas

作者：Benjamin J Callahan1, Paul J McMurdie,Michael J Rosen, Andrew W Han, Amy Jo A Johnson2 & Susan P Holmes1

杂志：Nature methods, published: 23 MAy,2016

DADA2是一个用于建模和纠正Illumina扩增子测序错误的算法（https://github.com/benjjneb/dada2）。

DADA2准确地推断出样品序列，并解决了仅1个核苷酸的差异问题。

在一些模拟社区中，与其他方法相比，DADA2识别出更多的真实变异并输出了更少的伪序列。

• 介绍

扩增子测序中一个很重要的问题是如何从在带有测序错误的情况下（很显然，基于OTU的方法没有考虑测序错误的因素），从而解析真正的生物学变异。该挑战促使人们开发了扩增子的错误校正方法。

在DADA2发表以前，尚无针对illumina平台的错误校正方法。

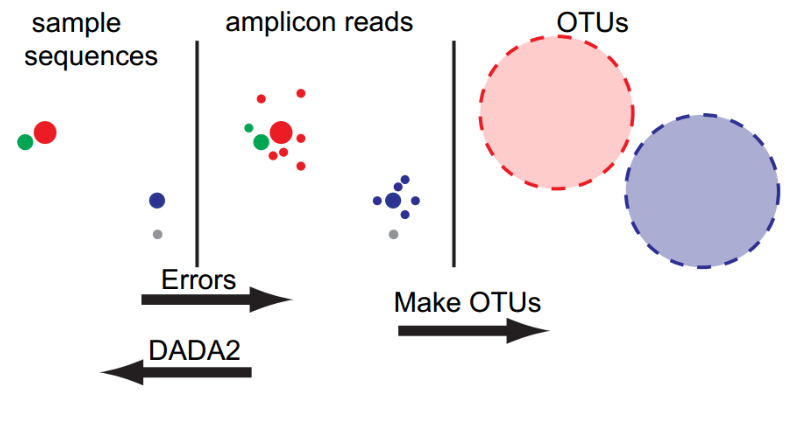
• otu方法的两大致命问题

目前，基于illumina平台扩增子测序错误的解决办主要是通过：先质量过滤，随后构建OTU来解决。

然而：

1.简单的根据相似度进行聚类会错把测序错误当做生物学变异，因此OTU的方法并没有进行假阳性推断。

2.此外，OTU方法没有利用测序错误模型，从而无法进行精细尺度变异（Fine-scale variation）的解析。

• 精细尺度变异与DADA2

精细尺度变异（Fine-scale variation）的好处很多。最浅显的：可以将某些菌株中的致病菌与普通菌株区分开，并且可以在复杂的微生物组相关疾病中提供更多的临床相关信息。

DADA2完整的扩增子工作流程：过滤，重复数据删除，样本推论，嵌合体识别以及成对末端读段的合并。

• 算法流程

1.根据error model计算error rate，error rate是量化了测序序列i产生自样本序列j的概率，error rate是序列碱基组成以及碱基质量的函数。

2.理论上，read i产生自read j的数量可以描述为泊松分布，期望值lambda= error rate x (# of read j)。如果i真的来自j，那么观测值（即，i的丰度）应当与期望值相等。根据这一事实，可以进行假设检验。计算的p-value记作abundance p-value.

3.abundance p-value被用于作为迭代partition算法的是否要继续迭代的阈值标准；当所有abundance p-value均满足阈值要求时，我们可以认为：同一个partition下的序列都产生于该partition的central sequence。最终，推算出来的sample组成就是每一个Partition中的center 序列以及对应的丰度。

【注：一个partition可以看做一个cluster，降噪体现在最后是以center序列作为partition的代表，这样就消除了partition内的其他序列由于测序原因而引入的错误。】

算法细节

error model

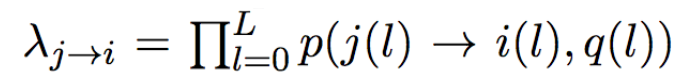
dada2假设在reads内的测序错误以及reads之间是相互独立的。

在这种假设下，样本真实的序列j产生测序序列i的错误率（error rate,即公式中的Lambda）可以描述为：每一个碱基替换概率的累乘函数。此函数与替换的碱基类型(也包含不发生替换的情况)，碱基测序质量得分有关。

例如，p(A→C, 35) 表示该碱基测序得分是35分的情况下，从A替换为C的概率（显然是一个很小的值）。

当然，在实际算法运行过程中，显然在起始条件下并不知道哪一条序列是真实的样本序列j，因此，采用启发式的策略，人为的把在一个partition下丰度最高的unique read假定为真实序列j,其他unique read与j进行比对，并计算相应的lambda(j->i)，(具体参考partition一节）。

如果序列j和序列i很相似，error rate应该是一个很接近1的值。如果两者匹配不上，那就直接把error rate分配为0。

abundance p-value

如果测序的错误在一段reads上是独立的，那么，真实的序列j产生测序序列i的数量应当服从泊松分布，其中测序序列i的期望值应当为：

期望值=error rate x 期望的样本真实序列j数量

error rate可以从error model计算得到

期望的样本真实序列j数量显然无法得到，但可以采用启发式算法进行迭代求解。（参考下一节）

根据这个期望值以及实际得到的观测值，我们就可以利用假设检验判断read i是否来自于序列j。

因此，进一步进行假设检验：

H0：测序序列i的观测丰度 = 理论期望值

H1：两者不相等

p-value可以用于衡量一条测序序列i产生自真实的样本序列j的可能性大小。

如果P-value很大，则无法拒绝原假设，我们就认为测序序列i是来自序列j，即i和j最后被划分为同一个partition；

计算p-value：

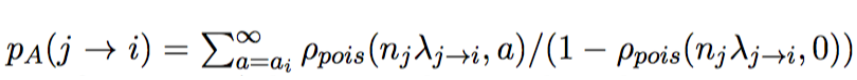其中：

j是假设的来自样本的真实序列，i是测序序列，n_j是期望的样本真实序列j数量，lamda是error rate，a_i是read i的实际观测值。

n_jxlambda就是真实的序列j产生测序序列i的数量的期望值。

个人的思考：

p-value的定义：the probability we get this sample and a more extreme sample under H0.

因此，根据p-value的定义：在本例子下，我们的p-value可以计算为：序列i的丰度观测值a_i以及更多的情况下的概率。

所以，原论文中Then, conditional on i being read at least once, the abundance pvalue is the probability of seeing nj or more identical reads 的表述应该是错误的。

公式中的分母：

可以这么解释：

除以1- p(0)是为了剔除掉观测值为0的情况（显然，观测值不可能为0）。由于概率分布之和为1，因此除以1-p(0)进行重新归一化。

显然，p-value越小，越表明现有的reads丰度无法被error model所解释，也就意味着这个测序序列i不是来自于该真实序列j(再一次强调，在实际算法运行过程中，显然在起始条件下并不知道哪一条序列是真实的样本序列j，因此，采用启发式的策略，人为的把丰度最高的unique read假定为真实序列j,其他unique read与j进行比对，并计算error rate 以及进一步根据error rate计算abundance p-value)

注意：

1.p-value显然需要一个阈值，用于判断是否显著，这个值通过OMEGA_A 参数进行设定，默认：1e-40。

2.启发式算法采用迭代策略，直到所有partition内的abundance p-value都大于阈值。

3.singleton 的p-value被设定为1，并且不会被error model判断与真实序列j的一致性。这意味着，singleton无法构建partition（具体参考partition:分配算法一节），因此DADA2不会推断singleton

partition:分配算法

前面一直提到：在实际算法运行过程中，显然在起始条件下并不知道哪一条序列是真实的样本序列j，因此，采用启发式的策略，人为的把丰度最高的unique read假定为真实序列j,其他unique read与j进行比对，并计算error rate 以及进一步根据error rate计算abundance p-value)。

具体的分配步骤：

1.扩增序列被进行去冗余，从而得到若干unique reads;每一个unique read可以根据原始reads数量换算成丰度，以及求取平均质量。（平均质量需要被用于error model）

2.将所有unique reads分配到一个partition中，将丰度最高的read分配为中心。

人为将丰度最高的reads作为中心，并假设为真正来自于样本序列，个人认为这是因为：

由于聚类过程是根据完全一致性进行unique reads划分，这个过程很显然，由于测序的错误，许多本是来自于同一个样本序列的reads会被划分为不同的unique reads；而丰度最高的unique reads显然可信度是最高的，因此也可以认为这个unique reads与样本真实序列是最近的。

其他所有unique reads与中心read进行比对，计算error rate： lambda(center->each unique read)，以及进一步计算abundance p-value。

3.如果最小的p-value(经过bonferroni校正)小于用户设定的阈值OMEGA_A （根据经验设定，默认是），这就表明算法认为该partition中仍然存在着不是来自于真实序列（partition center)的测序reads；此时，将继续创建一个新的partition,并把p-value最小的reads分配为新的中心，其他所有unique reads与新的中心逐一进行比对,一旦发现新的中心更可能产生该unique reads，那么就把该unique reads划分为新的partition。

4.第3步不断进行迭代，直到所有的p-value都大于OMEGA_A 。此时，可以认为，每条序列已经被划分为最可能产生它的partition中。

最终，根据1-4步推算出来的sample组成就是每一个Partition中的center 序列以及对应的丰度。（降噪体现在最后是以center序列作为partition的代表，partition内的其他序列由于测序错误的原因，最后直接被忽略了）

error model的参数

前面提到的error model中的替换概率问题，error rate的计算依赖于每一个碱基替换的概率，而每一个碱基的替换情况由于实际碱基测序质量有关。

因此，实际上存在16x41个参数

41代表了所有质量得分情况（1~41），16是4种碱基替换情况，见下图：

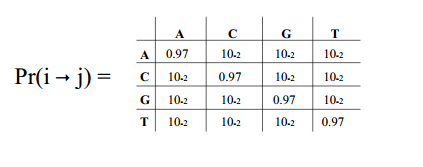
因此DADA2提供了3种选择：

1.基于用户的实际数据进行参数估计（利用dada2内置算法selfConsist ）

2.（默认）单独对每一种替换，进行基于weighted loess 的拟合

regularized log (observed mismatch rates ) ~ weighted loess function(mismatch base quality)

3.用户自己定义一个参数估计函数。

测评

• benchmark

与4种算法进行了比较：

UPARSE

MED

mothur（平均链接）

QIIME（uclust）

• 模拟社区

在模拟社区进行了测评：Balanced，HMP和Extreme

平衡的社区包含在理论上相等的频率：57种细菌和古细菌。

HMP社区包含21个细菌在名义上相等的频率17，

而极端群落包含27个细菌菌株，其频率跨越五个数量级，在整个序列区域上相差至少1个核苷酸（nt）。

• 测评指标

将输出序列与组成这些模拟社区的参考序列进行了比较，根据算法结果，输出序列被分成了3种：

Exact hit: blast比对完全比对上了参考序列。

One-off:存在一个Mismatch 或者 gap。

Other：其他情况。

sensitivity ：定义为Exact hit的比例。（需要注意的是：由于精细尺度变异广泛存在于模拟社区中，因此有些参考的菌株在16s序列中包含了多个可以区分的序列变异。）

DADA2软件流程

分裂扩增子去噪算法（Divisive Amplicon Denoising Algorithm.）

考虑了测序质量，无需参考数据库。

核心降噪算法是基于Illumina测序错误模型。

1.过滤： fastqFilter()

与usearch fastq_filter命令类似

此函数将序列修剪为指定的长度，删除短于该长度的序列，并根据歧义碱基的数量、最低得分、reads中的期望错误进行过滤。

fastqPairedFilter() 实现了同样地功能，只不过输出的是前、后端都通过过滤的reads。

2.重复删除 ：derepFastq（）

derepFastq（）导入一个fastq文件并输出重复序列的唯一序列及其丰度。

derepFastq（）还会输出一致序列的碱基质量得分（通过计算一致序列中对应位置的碱基质量平均值。）

该质量得分用于error model的dada函数。

3.降噪：dada()

细节在前面已经描述。

4.去除嵌合体：isBimeraDenovo()

去除嵌合体最好dada()之后，推断样本系列之前进行。

而且，最好不要使用独立的嵌合体去除算法（因为当前大多数独立的嵌合体识别程序，在识别与其他更丰富序列时更加保守，因为此类序列有望在以后合并在同一OTU中）。

具体实现：

首先，嵌合体所来源的序列丰度一定要比嵌合体大。

因此，嵌合体序列是通过与丰度更高的序列进行Needleman-Wunsch 全局比对发现的，如果嵌合体的左端或者右端能与母序列毫无差别的匹配上，就认为是嵌合体。如果嵌合体序列与母序列存在单个碱基/indel的差别，也会被标记。

5.合并双端序列mergePairs()

如果两段序列确实存在overlapp,就merge起来。注意到在DADA2管道中合并是在去噪后，因此严格要求精确重叠（因为预几乎所有替代错误都已经已被降噪算法删除）。

• 注意事项

1.降噪后再合并双端序列

这是因为核心去噪算法使用了质量得分和错误率之间的经验关系。如果序列合并过后，正向，重叠和反向序列部分的这种关系会变得不一致，从而干扰降噪算法。

补充1：精确序列变异缘何替代OTU？

用精确序列变异取代OTU，这样能够使标记基因测序：

1.更加有效精确（去噪算法），

2.可重复使用（即使更多的样本进来了也不需要重算），

3.可再现且全面（不同研究之间具有可比性）。

精确序列变异有很多种叫法，都是一个意思：

Exact Sequence Variants (ESVs)

• Callahan et al. 2017 (by accident)

Amplicon Sequence Variants (ASVs）

• Needham et al. 2017
• Callahan et al. 2017

sub-OTUs (sOTUs)

• Amir et al. 2017

Zero radius OTUs (zOTUs)

• Edgar 2017

Haplotypes, oligotypes, …

其中zOTU的叫法可以形象的用下图描述：

参考

论文：dada2: high-resolution sample inference from illumina amplicon data

slides：https://www.biostat.washington.edu/sites/default/files/modules//2016-SISMID-14-01.pdf